 From the Book on Harmonics by Hans Kaiser.
The general concept of this chapter is that there is the possibility to find, obtain and build sonorous images, meaning that they can be perceived both by the eyes and by the ears at the same time. From the Book on Harmonics by Hans Kaiser.
The general concept of this chapter is that there is the possibility to find, obtain and build sonorous images, meaning that they can be perceived both by the eyes and by the ears at the same time.
Sonorous images
Subject:Mysteries of the Builders
Sonorous images
From the Book of Harmonics by Hans Kaiser
The general concept of this chapter is that there is the possibility to find,
obtain and build sonorous images, meaning that they can be perceived both by
the eyes and by the ears at the same time.
We are not talking, mind you, about connotations similar to the musical notes
or any other written form of the word. Of course we could use completely different
signs from those normally used (c, d, e, f, …).
The geometric nature of Harmonics wouldn’t be affected by this.
This is the core of the sonorous figures, where sonorous and numerical proportion
finds direct expression.
The consequence is that any harmonics diagram is a sonorous image.
Sonorous images involve three senses at the same time: touch
(numbers and measures), sight and hearing (sounds)
and they join in a mental act.
As its application, the Author proposes the study of the sonorous image
of the human image, showing at first its external harmonious proportion
and then its sonorous content.
This research goes back to old times.
The Author reminds us of the human figures drawn by the Egyptians, the
famous Canon of Polykleitos, the rules of Italian
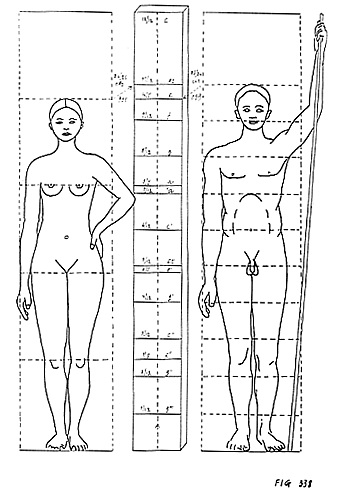
Renaissance. He refers to (fig. 338) the study by Wineken
on the proportions of the male and female human body.
As you can see in the image, man’s height is divided into twelfths
– viz. in fifths; woman’s height is divided in thirds (*). |
 |
__________
(*) The interval is the distance between two sounds. Any interval is expressed
by a number that establishes the relation existing between two sounds.
For example: C-D, interval of a second; C-A, interval of a fifth. The interval
is calculated according to the succession of our notes, counting the initial
note and the final note and implying the intermediate notes.
For example: C-G= interval of a fifth, C (D, E, F) G
__________
In this case the division in twelfths means the formation of an interval of
a fifth calculated according to the development of harmonic sounds where, taking
as fundamental note C, the twelfth harmonic is a G, viz. a sound with an interval
of a fifth.
The division in fifth means the formation of an interval of a third, again
calculated according to the development of harmonic sounds. The harmonics according
to the note C are the following:
| Harmonics |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| Notes |
C1 |
C2 |
G3 |
C3 |
E |
G3 |
Bb3 |
C4 |
D4 |
E4 |
F# 4 |
G 4 |
Therefore the relation between the two is:
| man |
: |
woman |
|
| 5/6 |
: |
4/5 |
25 / 24 |
This is a relevant result, being the relation between a major third (4/5
ex; woman) and a minor (5/6 ex; man) (*), which confirms
the importance of the number five with regard to sex.
If we take the C as a basis, we have the following values:
Woman : Man |
Man : Woman |
4/5 : 5/6 |
5/6 : 4/5 |
= 24 / 25 C cis |
= 25 / 24 C ces |
__________
(*) The interval of major third is always calculated according
to the succession of harmonics sounds. Between C 3 and E 3, viz. between the
forth and fifth harmonics (45), an interval of major third, namely an interval
made by two tones, is created. The interval of minor third (made by a tone and
half) is between the fifth and sixth harmonics, viz. between E 3 and G 3.
__________
Therefore the relation would be: ces (C) cis (*)
It looks like the relation man/woman, in the sense of harmonics, originates
two chromatic notes (**), symmetric to the fundamental (C)
almost as if the two bodies were both generated by a unique androgen unmanifested
reality.
__________
*) The word ‘ces’ corresponds to C flat (Cb), whilst the word ‘cis’
stands for C sharp (C#).
(**) By chromatic notes we mean two notes at a distance of a semitone that keep
the same name. For example: C-C#, or C-Cb.
__________
The Author carries on by examining the figure of the female body (fig. 339)
through the method of equitonals, and he concludes
that its main points and parts are determined by lengths that, together, make
the common diatonic musical scale:
c d e f g a h c (*)
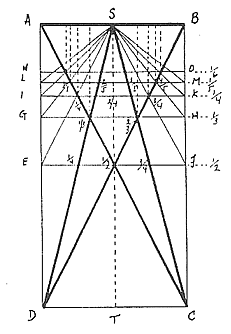
Still with regards to the human figure, he considers the Canon of Villard
by Honnecourts, further harmonics divisions, whose construction is reported
below (**):
__________
(*) this is the transcription in Italian of the musical notes:
| C |
D |
E |
F |
G |
A |
H |
(B) |
| Do |
Re |
Mi |
Fa |
Sol |
La |
Si |
(Sib) |
(**) Kaiser dedicated a special leaflet to this canon used by the Builders
of Cathedrals of the middle Ages. You can see an extract mentioned in this Commentary,
page 144.
__________
Be A B or CD the segment to divide. Let’s
draw a rectangle with proportions 1:2.
Now let’s draw the diagonals AC, DB
and the angle DSC; we already have Villard’s scheme.
It offers us two values of parts:
1) At the intersection of the diagonals, half (1/2
of the segment) AB;
2) At the intersection of the diagonals with the oblique
SC, SD the division by three of the segment AB or
more precisely the points 1/3 e 2/3.
The rest follows automatically.
Let’s draw from the point of intersection of the
diagonals the parallel to the line AB and we obtain the
points E and F.
The lines SE and SF give, with their intersection with
the diagonals, the division by 4 (1/4 e 3/4). Then we
draw from 1/3 and 2/3 the parallel GH,
the lines SG and SH; this gives us,
at the points of intersection with the diagonals, the division by 5
(1/5 e 4/5).
In theory, we could continue the division endlessly and obtain all the
rational division of the segment AB.
This method of distribution as it appears in fig. 341 has the advantage
of allowing not only vertical division, but also horizontal ones, not
examined by the mentioned Wyneken.
We refer to the thorough exam of the figure to observe the harmonious
disposition of both the external image of man and his main organs (heart,
head, etc.).
|
 |
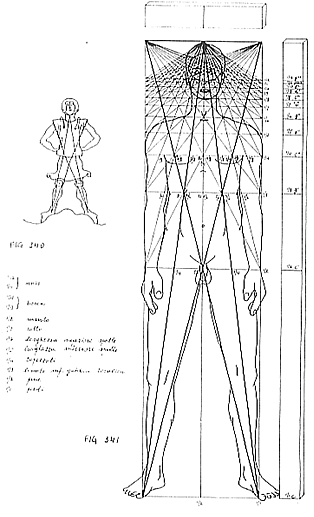
The examples discussed so far have been examined from the outside
to the inside; that is starting from the (human) figure,
of which we have taken measurements and relations.
There is another method for harmonic research: from the inside
to the outside.
It means to follow, through the growth of a harmonic configuration,
what can be the next growths of the biological form, through a Generator.
It means to observe models, impulses and images occurring with the progressive
increase of the Index. Some examples can be found in ‘Harmonia
Plantarum’; another is shown in the following pages: the
object is the human biological figure.
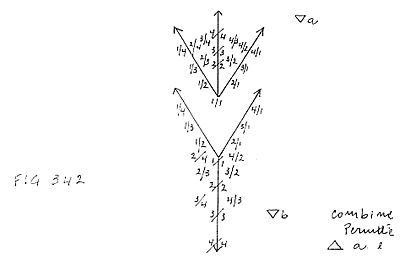
We start from an assumption. We take as a means a combination of the
triangular Diagram (see fig. 342), we fix as maximum index the number
12 and as generator all the numbers of the senary. |
The stages of the construction are the following (fig. 343, 344, 346, 349 and
350).
Index 1. Original, undifferentiated
cell.
Index 2. Both octaves (*) C' and
C appear; they are the axis of vertical symmetry and the two
tonal higher directions. Nothing new in the tonal sense.
Index 3. Two new sounds appear. G and
F, the dominant (**).
Index 4. No new sounds; other octaves.
|
 |
__________
(*) By octave we mean the interval between two notes with the same name, implying
the other seven internal notes. For example C (D, E, F, G,
A, B) C; 1 (2 - 3 - 4 - 5 - 6 - 7) 8
(**) The notes G and F are considered, in our musical system, as dominant notes
in the C major scale. Dominant means in general a note with a particular ‘tension’
in a scale and in a musical composition.
__________
In a figurative sense the two lower directions appear;
the Author calls them static because they contain only identical tonal
values, C' and C. Therefore they are
opposite to the two mentioned above, which have a precise dynamic character.
Index 5. The major and minor thirds originate and the
possibility of major and minor chords.
Index 6. This index as well (2 x 3),
as all the even indexes, doesn’t produce any tonal news.
In the figure is outlined the whole of points and values obtained so
far, to highlight the closed nucleus of the senary.
It is important to observe the melody made by perimetric sounds followed
in order: it is the melody of the border. We must say that every index
is characterized by its own melody.
Index 7 has been excluded, because of the law of the
Generator.
|
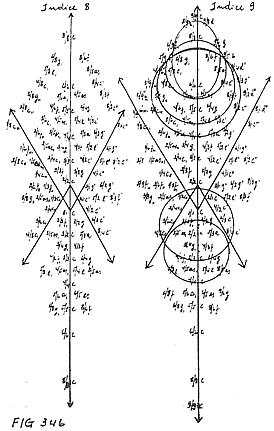 |
Index 8. A certain spatial structure appears for the first
time. The points are not closed tight, one against the other any more. In the
form we can see open spaces.
Nothing new in a tonal sense (except for the melody of the border!)
Index 9. The sounds D and B
originate. The intervals of a second, so far absent, appear. The consequence
is the possibility to trace circles and ellipses of musical scales, such that
the sounds of their border are like a concluded musical scale.
Furthermore, this index originates a contest of counterpoint (intended
in its genuine sense); at this stage a specific differentiation enters
the biological form.
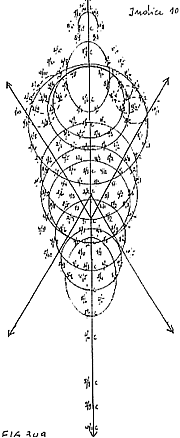
Index 10. No new sounds.
Two important aspects:
a) Three unfinished
musical scales, on the right and left sides of the axis of vertical
symmetry.
b) Two ellipses, at the top and bottom, containing the
first enharmonic sounds, namely places where
two sounds split inside the figure.
d__________d v
b__________b v
Index 11. Excluded because not relevant for the senary.
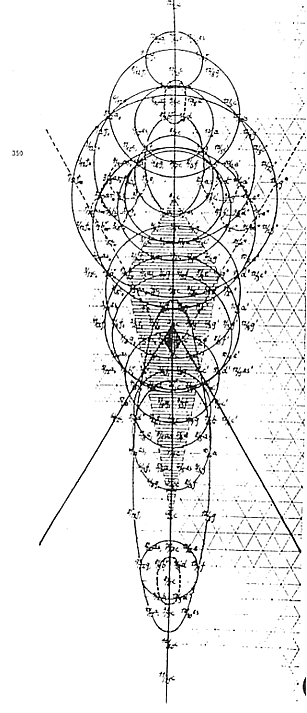
Index 12. (fig. 350) The form is for
the moment (because of our assumption) complete. The following observations
are due:
|
a) Axis of vertical symmetry.
It divides the form in two parts: greater than 1 and less than 1, right and
left. This explains the presence of two clearly distinct polarities in the human
form.
There is another polarity, though, present in every part of it: the major
and minor tone. The latter doesn’t depend at all on the simple numerical
expressions.
b) Two separate pairs of directional axis. The superior
one is dynamic, the inferior is static. The correspondence with the higher
and lower limbs of man, hands and feet, is obvious.
Note that the exam of the values and not of the numbers allows the understanding
of the different function of these pairs.
c) Sonorous circles on the left and the right and
in the higher part (3 + 3). They seem to represent the biological parallel of
the appearance of double sensorial organs (eyes, ears).
d) The central nucleus: true solar plexus
from which all directions and impulses irradiate. It is the true starting center
of the harmonic and morphologic development.
e) Counterpoint. Every sound present in a part of
the form has its exact counterpoint in the symmetric one. Furthermore, because
of the combination of two Diagrams chosen there is also congruence. In a biological
sense, this reality justifies and ensures the transformation of the organic
form; this is nothing but the material and visible expression of melody and
counterpoint.
f) Two central ellipses, high and low. We’ve
already talked about this with the Index 10.
It is justified to assume that they indicate the cerebral sphere
and the sexual function. Their polar collaboration in the whole of
the form is obvious; their true harmonic meaning, though, is visible only by
observing their sonorous content.
Where the first enharmonic divisions appear in the sonorous development, we
can find both; around a center of identical value (C) two different values of
B and D appear.
The enharmonic structure that they have seems to indicate the deep need for
a dialectic motion of the two spheres of action, in and between
themselves.
The Author warns that when we want to study
in such a way the growth of an organic form or when we want to verify
its harmonic impulses, we can’t expect exact results.
These sonorous figures show and reveal the inner tendencies of development.
It is not about finding through them the formal differences between hand
and foot, but about discovering their psychic reciprocity.
Another consideration is that melodics occur (becomes in a certain
period) whilst a chord is, whilst it coexists spatially. Furthermore,
in the formal expression melodics can be assimilated by graphic or a drawing;
the chord, on the opposite, is similar to the pictorial or the coloristic
whole.
As an example of ektypic application, the Author proposes the Canon
by Villard by Honnecourt, examined and discussed earlier.
He points out that if we develop it in the senary, we keep constant
the basis and vary the height in the measure of 1/2, 1/1, 2/1,
we obtain three figures (427) that can describe the essential outline
of three completely different architectonic styles.
|
 |
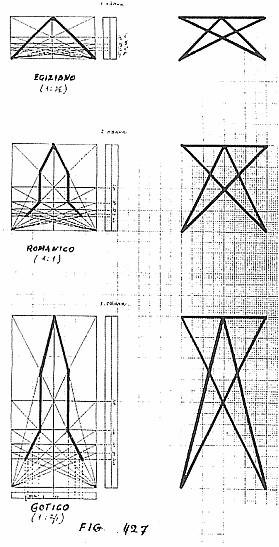 |
Egyptian, Romanic and Gothic.
In the first the earth prevails, in the second we have a balance,
whilst in the third the celestial element prevails.
Three octaves, three styles, three civilizations.
|
|


